三重积分之大爷不会画图

高数叔 · 发表于 2020-4-9 18:50:00

开篇语

对于三重积分的计算，有很多同学抱怨说：“姑姑！你讲三重积分的计算，无论是直角坐标的先一后二方法还是柱面坐标，都要先求出投影区域，然后还要通过穿入面和穿出面找 z 的积分限，但可是，大爷我特么不会画图怎么办？我怎么知道你随便找俩长得像洗脸盆一样的图扣在一起的积分区域长成什么样？”那么好，今天叔就不画图，来告诉你们对于两个脸盆扣出来的积分区域，它的投影区域怎么求，积分限又怎么算，咱们没有画画的艺术细菌，还能没有解方程的初中文凭么！

根据叔多年经验掐指一算再上网一查，有几个曲面，也就是你们说的洗脸盆，经常在三重积分的题目中出镜，属于一线名脸盆。它们就是球面、抛物面和锥面，这三大名脸盆经常两两组合在一起围成积分区域，下面我们就分情况说明投影区域和积分限怎么求。

有木有豁然开朗！别急，还有几种情况：

由这三个常见曲面组合围成的积分区域，基本就是上述这几种情况。很多学霸可能会说，这三类曲面我太熟了，画出图来岂不是更好算。那么好，下面我们再来介绍一种你们不太熟悉的情况，不画图更更好算：

如果学霸们觉得上面几种情况都不过瘾，也都还能用画图的方法直观找出积分区域，轻松解决问题，那么接下来，叔就要祭出大神曲面——马鞍面：

z=xy

还！有！谁！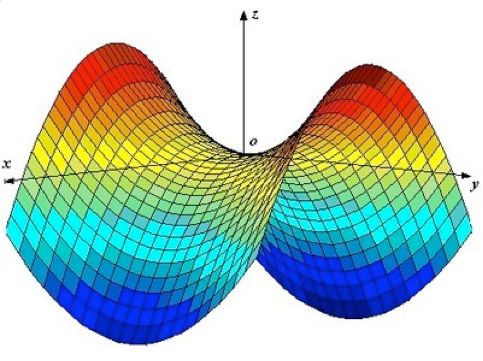

专治各种强迫症

画个图能要人命

不画图也能搞定

看几个题压压惊

三重积分秘籍就讲到这里，相信大家不会再那么恐惧了，快去找几个题试试手吧！

大爷不会的姑姑会

▼

- END -

版权说明：内容来自高数叔原创，文字、图片及视频已经申请版权保护，根据《中华人民共和国著作权法》、《中华人民共和国著作权法实施条例》、《信息网络传播权保护条例》等有关规定，如涉版权问题，请与我们联系，谢谢！

		记住	找回密码
密码			加入慢享